You know you’re studying functions when you hear “one to one” more often than you ever had. Curious about what makes one to one functions special? This article will help you learn about their properties and appreciate these functions. Let’s start with this quick definition of one to one functions:
One to one functions are functions that return a unique range for each element in their domain.
Since one to one functions are special types of functions, it’s best to review our knowledge of functions, their domain, and their range.
This article will help us understand the properties of one to one functions. We’ll also learn how to identify one to one functions based on their expressions and graphs.
Let’s go ahead and start with the definition and properties of one to one functions.
To easily remember what one to one functions are, try to recall this statement: “for every y, there is a unique x.” The next two sections will show you why this phrase helps us remember the core concept behind one to one functions.
The function, f(x), is a one to one function when one unique element from its domain will return each element of its range. This means that for every value of x, there will be a unique value of y or f(x).
Why don’t we visualize this by mapping two pairs of values to compare functions that are not in one to one correspondence?
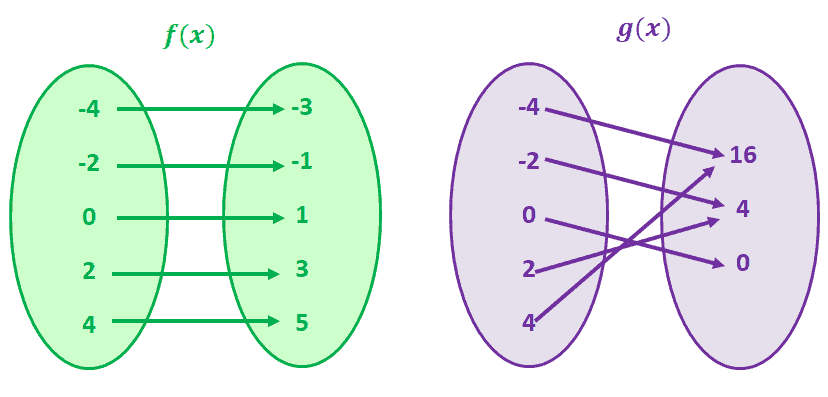example of one to one function" width="828" height="397" />
Let’s take a look at g(x) first, g(4) and g(-4) share a common y value of 16. This is also true for g(-2) and g(2). You guessed it right; g(x) is a function that does not have a one to one correspondence.
Now, observe f(x). Notice how for each f(x) value, there is only one unique value of x? When you observe functions having that correspondence, we call those functions one to one functions.
To better understand the concept of one to one functions, let’s study a one to one function’s graph. Remember that for one to one functions, each x is expected to have a unique value of y.
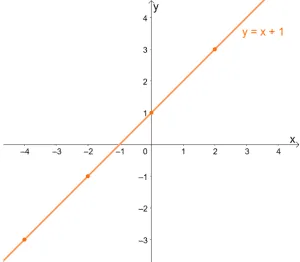
Since each x will have a unique value for y, one to one functions will never have ordered pairs that share the same y-coordinate.
Now that we’ve studied the definition of one to one functions, do you now understand why “for every y, there is a unique x” is a helpful statement to remember?
What are other important properties of one-to-one functions we should keep in mind? Here are some properties that can help you understand different types of functions with a one to one correspondence:
Try to study two pairs of graphs on your own and see if you can confirm these properties. Of course, before we can apply these properties, it will be important for us to learn how we can confirm whether a given function is a one to one function or not.
The next two sections will show you how we can test functions’ one to one correspondence. We are sometimes given a function’s expression or graph, so we must learn how to identify one-to-one functions algebraically and geometrically. Let’s go ahead and start with the latter!
Remember that for functions to be one to one functions. Each x-coordinate must have a unique y-coordinate? We can check for one to one functions using the horizontal line test.
What if it passes two or more points of a function? Then, as you may have guessed, they are not considered one to one functions.
To better understand the process, let’s go ahead and study these two graphs shown below.
The reciprocal function, f(x) = 1/x, is known to be a one to one function. We can also verify this by drawing horizontal lines across its graph.
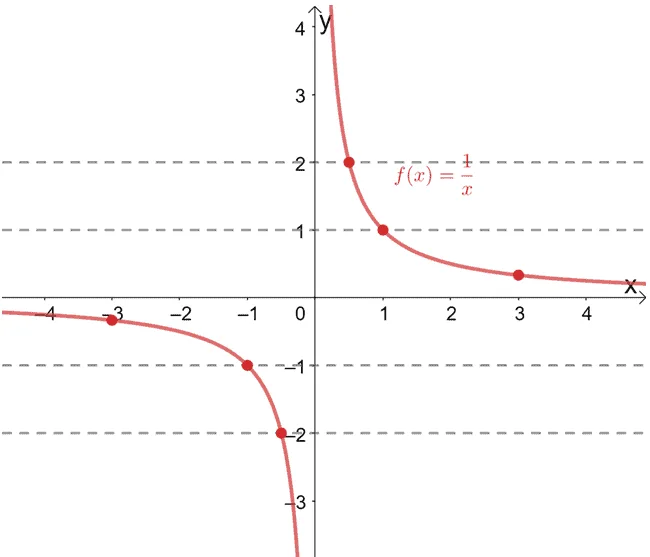
See how each horizontal line passes through a unique ordered pair each time? When this happens, we can confirm that the given function is a one to one function.
What happens then when a function is not one to one? For example, the quadratic function, f(x) = x 2 , is not a one to one function. Let’s look at its graph shown below to see how the horizontal line test applies to such functions.
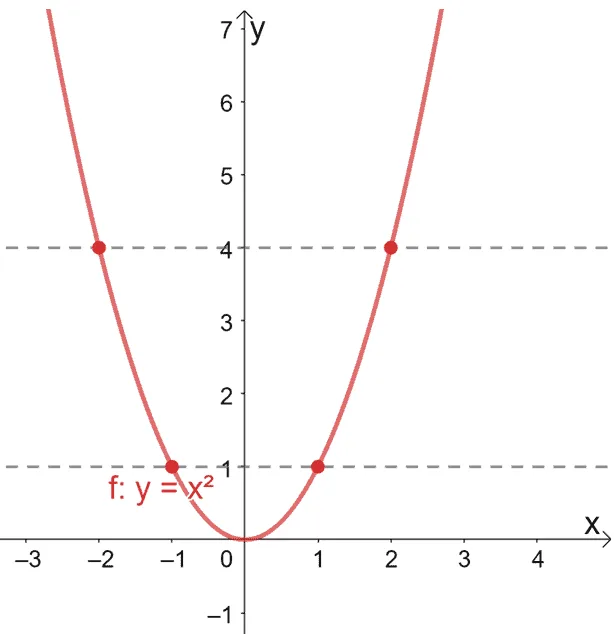
As you can see, each horizontal line drawn through the graph of f(x) = x 2 passes through two ordered pairs. This further confirms that the quadratic function is not a one to one function.
Let’s refresh our memory on how we define one to one functions. Recall that functions are one to one functions when:
We’ll use this algebraic definition to test whether a function is one to one. How do we do that, then?
Why don’t we try proving that f(x) = 1/x is a one to one function using this method?
Let’s first substitute x1 and x2 into the expression. We’ll have f(x1) = 1/x1 and f(x2) = 1/x2. To confirm the function’s one to one correspondence, let’s equate f(x1) and f(x2).
Cross-multiply both sides of the equation to simplify the equation.
We’ve just shown that x1 = x2 when f(x1) = f(x2), hence, the reciprocal function is a one to one function.
Example 1
Fill in the blanks with sometimes, always, or never to make the following statements true.
When answering questions like this, always go back to the definitions and properties we just learned.
Example 2
Let A = and B = . Which of the following sets of ordered pairs represent a one to one function?
For a function to be a one to one function, each element from A must pair up with a unique element from B.
This means that represent a one to one function.
Example 3
Which of the following sets of values represent a one to one function?
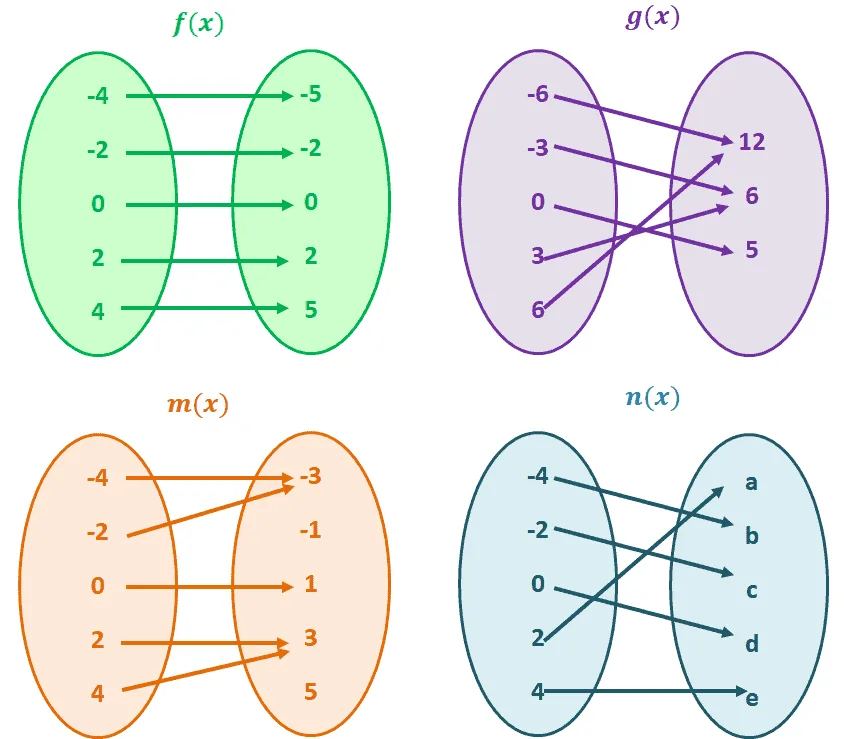
Always go back to the statement, “for every y, there is a unique x.” For each set, let’s inspect whether each element from the right is paired with a unique value from the left.
Example 4
Graph f(x) = |x| + 1 and determine whether f(x) is a one to one function.
Construct a table of values for f(x) and plot the generated ordered pairs. Connected these points to graph f(x).
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(x) | 4 | 3 | 2 | 1 | 2 | 3 | 4 |
The table alone can already give you a clue on whether f(x) is a one to one function [Hint: f(1) = 2 and f(-1) =2]. But let’s go ahead and plot these points on the xy-plane and graph f(x).
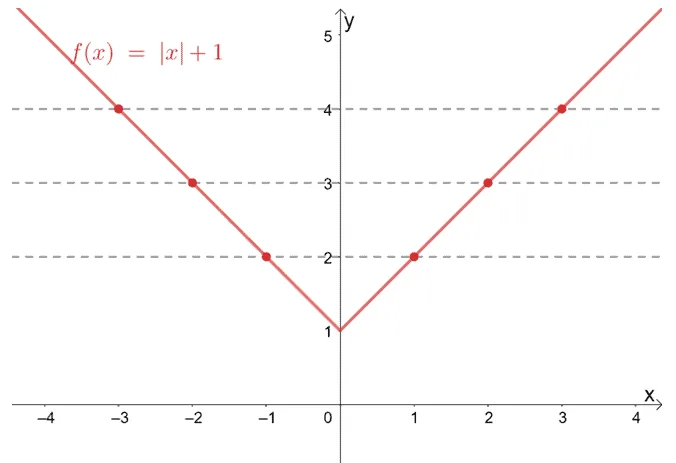
Once we’ve set up the graph of f(x) = |x| + 1, draw horizontal lines across the graph and see if it passes through one or more points.
From the graph, we can see that the horizontal lines we’ve constructed pass through two points each, so the function is not a one to one function.
Example 5
Determine if f(x) = -2x 3 – 1 is a one to one function using the algebraic approach.
Recall that for a function to be a one to one function, f(x1) = f(x2) if and only if x1 = x2. For us to check if f(x) is a one to one function, let’s find the respective expressions for x1 and x2 first.
Equate both expressions and see if it reduces to x1 = x2.
Taking the cube root of both sides of the equation will lead us to x1 = x2. Hence, f(x) = -2x 3 – 1 is a one to one function.
Example 6
Show that f(x) = -5x 2 + 1 is not a one to one function.
Another important property of one to one functions is that when x1 ≠ x2, f(x1) must not be equal to f(x2).
A quick way to prove that f(x) is not a one to one function is by thinking of a counterexample showing two values of x where they return the same value for f(x).
Let’s see what happens when x1 = -4 and x2 = 4.
We can see that even when x1 is not equal to x2, it still returned the same value for f(x). This shows that the function f(x) = -5x 2 + 1 is not a one to one function.
Example 7
Given that a and b are not equal to 0 show that all linear functions are one-to-one functions.
Remember that the general form of linear functions can be expressed as ax + b, where a and b are nonzero constant.
We apply the same process by substituting x1 and x2 into the general expression for linear functions.
Equate both equations and see if they can be reduced to x1 = x2. Since b represents a constant, we can subtract b from both sides of the equation.
Divide both sides of the equation by a, and we’ll have x1 = x2. From this, we can conclude that all linear functions are one-to-one functions.
1. Show that $g(x) = |x| – 4$ is not a one to one function.
2. Show that all quadratic expressions are not one-to-one functions.
1. The absolute value function, $g(x) = |x| – 4$, has the curve as shown below.
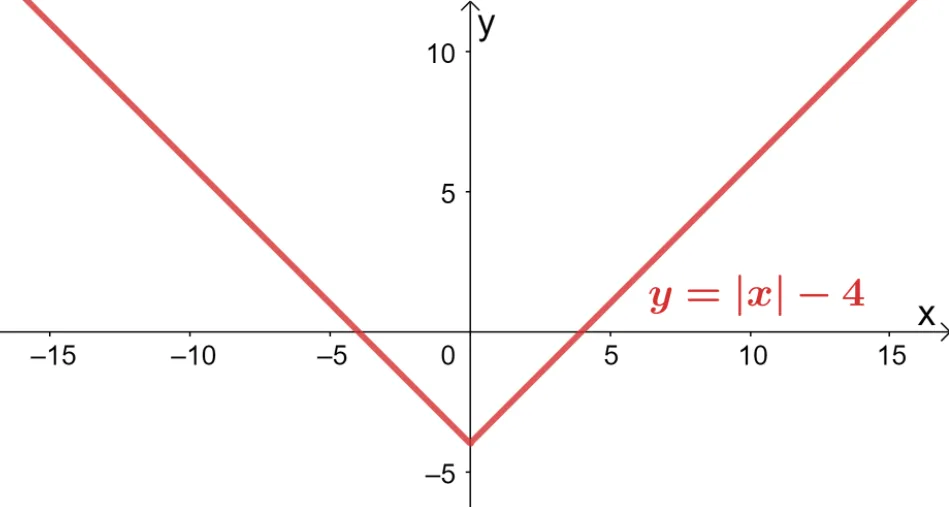
Using the horizontal line test, we can see that each horizontal line passes through more than one point.
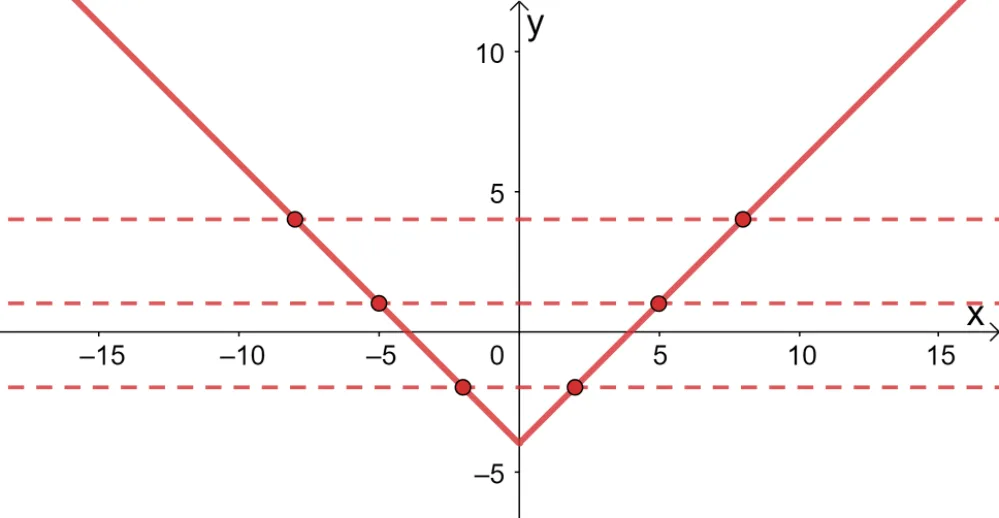
We can also use the algebraic approach to show that $g(x)$ is not an absolute value function. Simply think of a pair of points sharing the same $y$-coordinate and satisfying the function such as $(-6, 2)$ and $(6, 2)$.
2. The graph of a quadratic function will always be a U-shaped curve, so the curve will always fail the horizontal line test. This means that quadratic functions will never be a one-to-one function.
Images/mathematical drawings are created with GeoGebra.
